技術公差とは何か、どのように分類されるか？

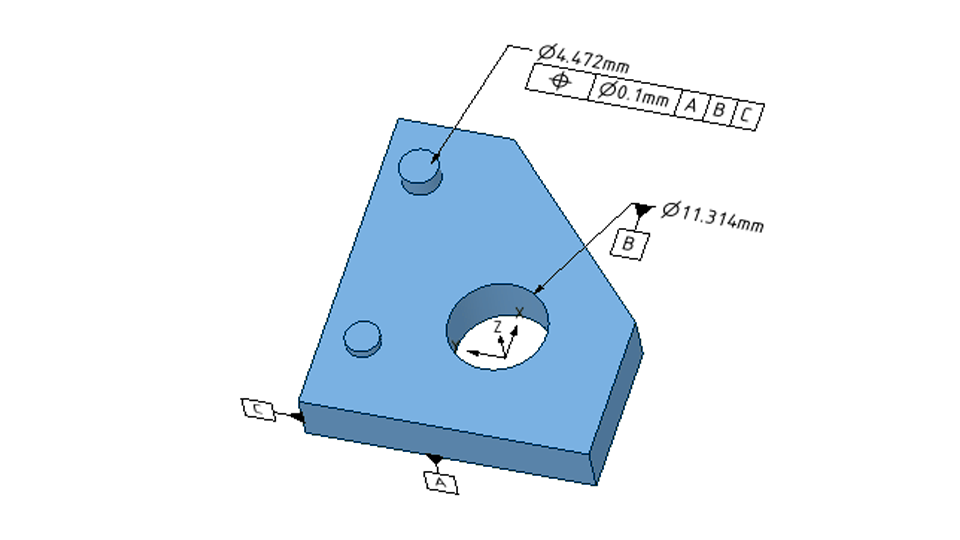
精度は、エンジニアリングと製造において非常に重要な側面です。指定された測定値からのわずかなずれが、部品の機能や性能に影響を及ぼす可能性があります。そこで、機械工学の公差が非常に重要になります。エンジニアリング公差は、部品の物理的寸法、形状、特性のばらつきの許容限度を定義します。これらの公差は、部品がアセンブリ内で適切に適合し機能し、最終製品が指定された要件を満たすことを保証します。公差は、特に自動車、航空宇宙、機械製造などの産業において、部品間の相互運用性を確保するために必要です。

本稿では、公差の分類とエンジニアリングにおける具体的な用途を中心に、さまざまなタイプの公差について説明する。

エンジニアリングにおける許容範囲とは？

公差とは、部品の実際の大きさ、形状、位置が、その理想的な大きさ、形状、位置から許容される偏差のことである。製造の過程では、機械の精度や作業手順などの要因により、実際の部品の大きさが設計の要求を完全に満たすことはできません。このような場合、部品の機能性や互換性を確保するために、ある範囲のずれが許容される。公差値は、許容値の上限と下限の差に等しい。

公差とは何かを説明するために例を挙げてみよう。長さ100mmの金属丸棒を加工するとします。すべて同じ形状に加工しようと思っても、サイズや形状のズレがあるため、すべての金属棒を100mmぴったりに加工することは不可能です。設計者や製造者はこのような偏差を減らす努力をしているが、それでも偏差をゼロにすることはできない。

このような寸法や形状の偏差は、基本的に目標値を中心に上下に変動する。そのため、金属棒の用途に応じて、目標寸法に対して許容される上限許容値（＋1mm）と下限許容値（-1mm）が決められています。この2つの値の差（2mm）を公差という。

寛容の種類

公差には4つの種類がある：寸法公差、幾何公差、はめあい公差である。各公差は、部品のさまざまな側面に焦点を当て、さまざまな作業環境において部品が適切な機能を持つことを保証します。

寸法公差

寸法公差とは、図面に記された寸法、すなわち長さ、距離、位置、角度、大きさ、開口部などの寸法に適用される公差を指す、 切り込みと面取りなど。一般公差とは異なる公差を示す場合に用いられる。寸法公差は、一般公差と異なり明確な基準がなく、設計者の意図により任意に規定することができるが、加工方法などにより実現可能な公差の範囲は限定される。寸法公差には、両側公差と片側公差の2種類がある。

二国間寛容

両側公差とは、基準寸法の両側で指定された範囲内に存在する寸法の許容変動を指す。言い換えれば、寸法は基準寸法に対して上下両方向に変動する可能性がある。

二国間寛容の例:穴の基本寸法が10mmで、両側公差が±0.05mmの場合、シャフトの実寸範囲は9.95mm～10.05mmとなります。

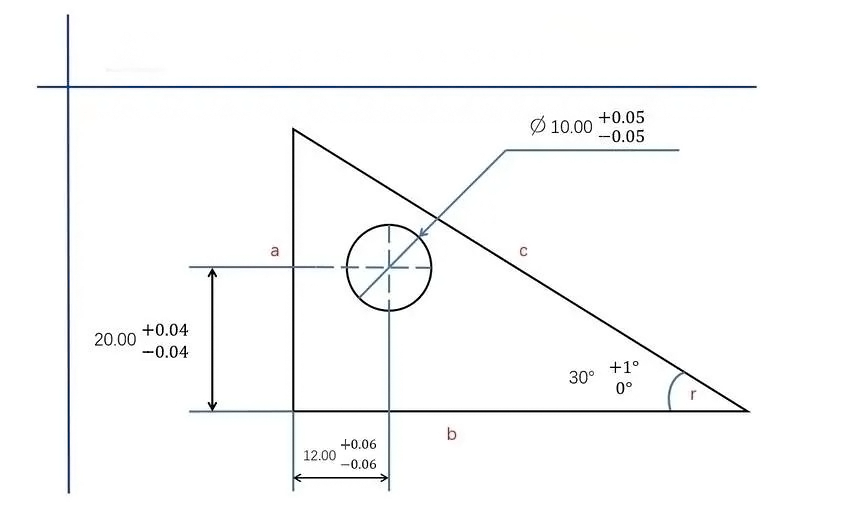
一方的な寛容

一方公差とは、基本寸法の片側のみに許容される寸法のばらつきを指す。

一方的な寛容の例： 穴の基本サイズが10mmで、片側公差が+0.05mmの場合、穴の実際のサイズ範囲は10.00mmから10.05mmとなる。

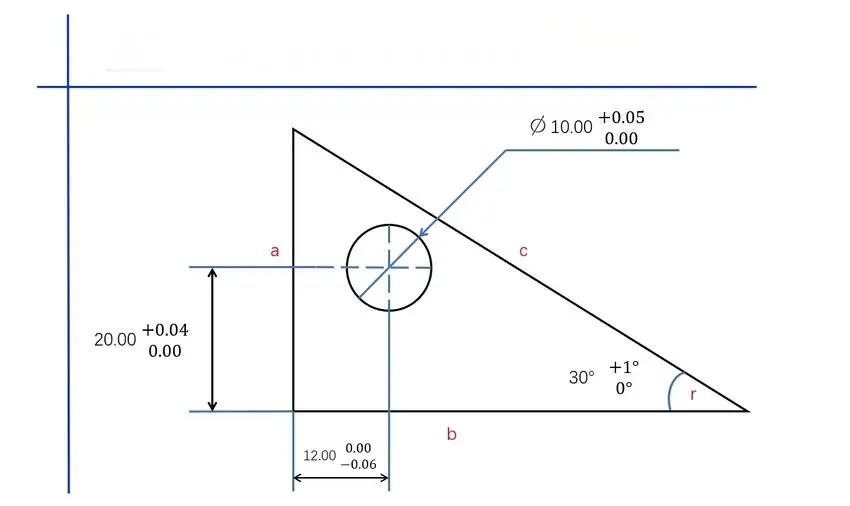
幾何公差

幾何公差は、部品の寸法を扱うだけでなく、部品の形状、位置、方向に関する精度も規定する。幾何公差は、部品の設計で規定された幾何学的形状の忠実性を保証するもので、一般的に真直度、平面度、真円度、位置精度などの属性で実施される。幾何公差の主な目的は、形状と位置の両方の精度を維持することであり、それによって部品の不適切な取り付けに関する問題を防止する。

幾何公差は、形状公差、方位公差、位置公差、振れ公差の4種類に分けられ、合計13種類になります。

直線性

直線性とは、指定された長さまたは表面における直線からの許容偏差のこと。部品の形状が完全な直線からどの程度ずれてもよいかを定義するために使用される。

直線性の例： ある平面において、検査される線分は、0.1mmの距離で2本の平行線の間になければならない。

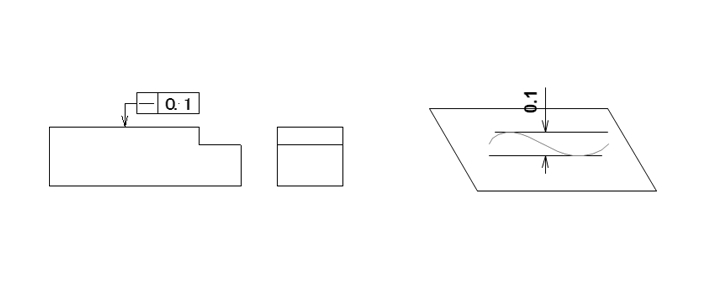
平坦性

平坦度は、理想的な平面からの表面のずれを定義する幾何学的条件である。理想的な平面からどの程度ずれているかを示す指標であり、表面の均質性を表す。

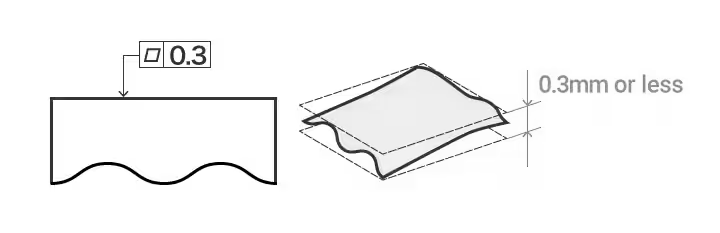
平坦性の例： この表面は、0.3mmだけ離れた2つの平行な平面の間になければならない。

丸み

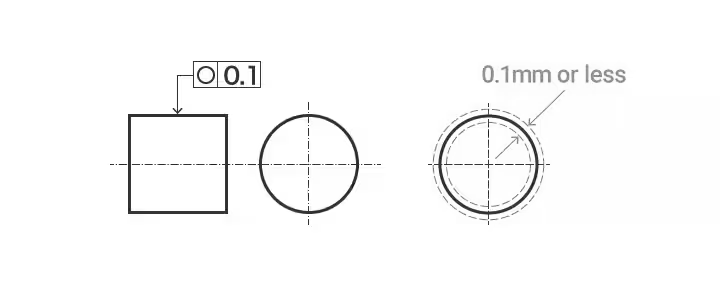
真円度は、一般に円形度とも呼ばれ、円柱、穴、球体などの形が、任意の断面において真円からどの程度離れているかを定義する幾何学的条件である。

丸みの例： シャフトを垂直に切断した断面の外周は、同一平面上で0.1mmだけ離れた2つの同心円の間に収まっていなければならない。

円筒度

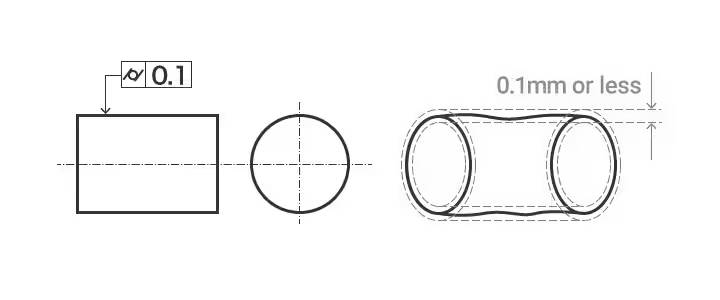
円筒度とは幾何学的な条件のひとつで、円筒形状の形状が理想的な円筒の形状にどの程度合致しているかを測るもの。円筒の長さ方向と円周方向における表面の均一性を測る。

円筒形の例： ターゲット面は、0.1mmしか離れていない2つの同軸円筒の間になければならない。

ラインのプロフィール

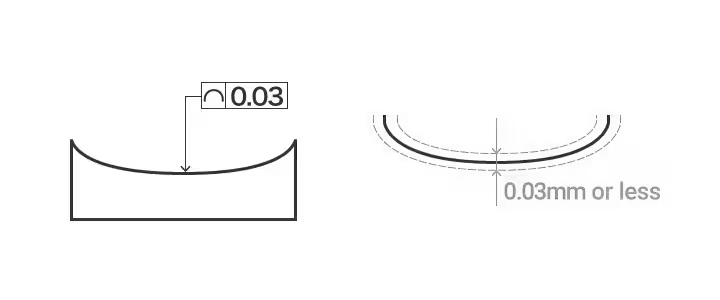
線の輪郭線は、部品の所定の平面上で、あらゆる形状の曲線の完全な形を保持するために必要な条件である。線の輪郭公差 非円形曲線の実際の輪郭線の許容偏差。

線の輪郭公差の例： 投影面に平行な任意の断面上の投影プロファイルは、理論的に正確なプロファイルを持つ線を中心とした直径 0.03 mm の円によって作られる 2 つの包絡線の間にあるものとする。

飛行機のプロフィール

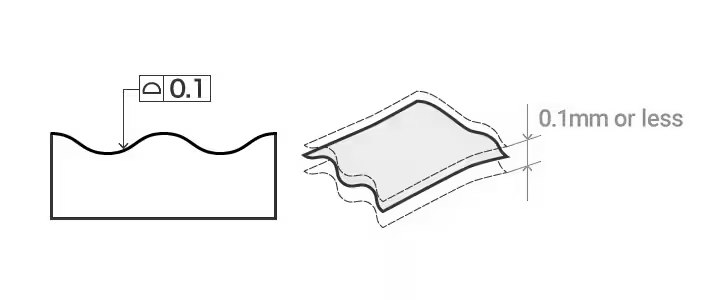
平面の輪郭とは、ある部品上のあらゆる曲面の理想的な形状を維持するための条件である。平面の輪郭公差とは、非円形曲面の実際の輪郭線が理想的な輪郭線から許容されるばらつきのことである。

平面のプロファイル公差の例： 仕向け面は、直径0.1mmの球が作る2つの包絡平面の間にあり、その中心は理論的に完全なプロファイルを持つ平面上にある。

パラレリズム

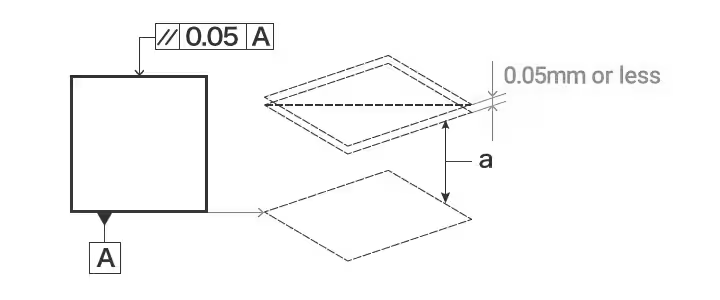
平行度とは、指定された基準（データム平面、軸、線など）から平行であることに関して、特徴（表面、軸、線など）が許容できるばらつき（偏差）のことである。平らさについて再び議論されているように見えるが、平行度にはデータム（基準面または基準線）が含まれる。

並列処理の例:指示矢印で示された平面は、基準面Aに平行で、指示矢印の方向に0.05mmだけ離れた2つの平面の間になければならない。

垂直性

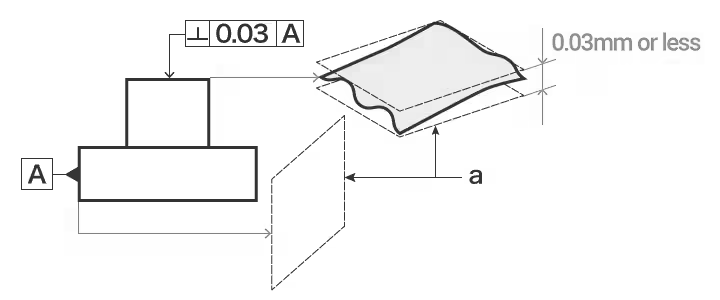
垂直性は幾何学的条件であり、面、軸、線などの特徴が、平面や軸を含む参照特徴に対して直角（90°）に整列している度合いを評価する。

垂直性の例： 指示矢印で表される平面は、基準面Aに直交する直径0.03mmの2つの平行面の間に位置するものとする。

アンギュラリティ

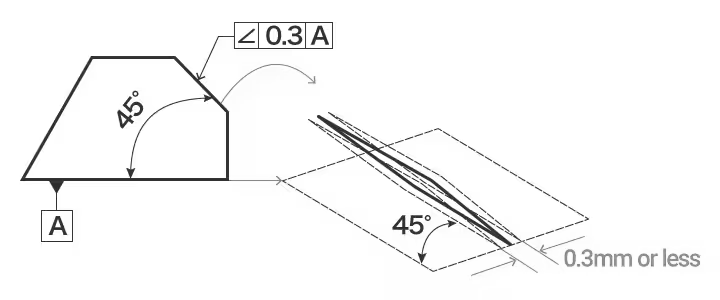
角度は幾何学的条件であり、表面、線、軸などの特徴が、基準データムに対して90°（垂直）または0°（平行）以外の指定された角度に向いている量を測定する。

角度の例： 指示矢印が示す平面は、基準面Aに対して理論上正確に45度の角度をなし、指示矢印の方向に0.3mmだけ離れた2つの平行な平面の間になければならない。

ポジション

Positionは、コンポーネントのポイント、ライン、サーフェスのリファレンスに対する正確な位置を見つけるために使用されます。

ポジションの例 について 表示矢印が示す円の中心は、直径0.1mmの円内にあること。

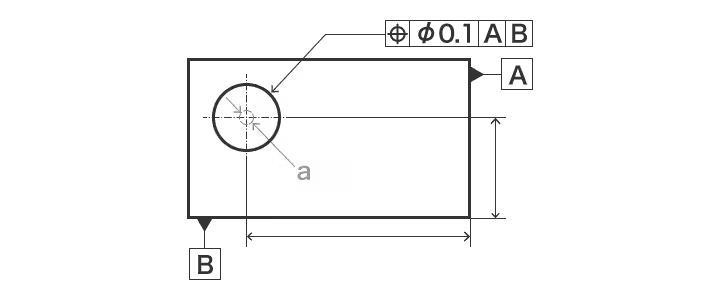
同軸性

同軸度は、シャフト、穴、管などの円筒形形状の軸が基準データムの軸と正確に一致することを保証する。

同軸性の例： 所定の円柱の軸は、データム軸線Aを軸とし、直径0.03mmの円柱内にあるものとする。

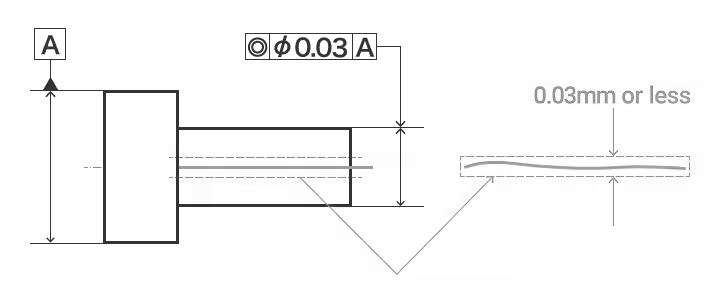
シンメトリー

対称性とは、ある特徴（または特徴の集合）が、中心となる基準軸、平面、または点に対してどの程度均等に分布しているかを測るものである。

対称性の例： マークされた中心面は、データム中心面 A に対して対称で、0.05mm 離れた 2 つの平行な平面の間とする。

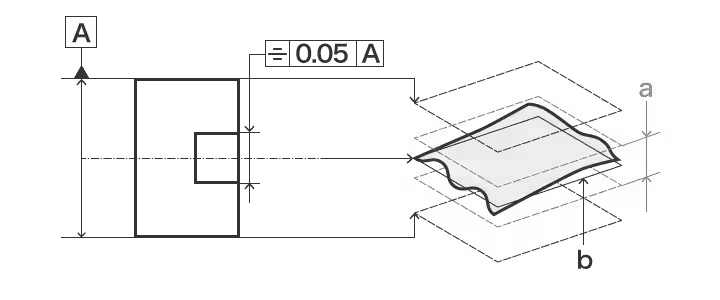
ランナウト

振れとは、フィーチャーが基準軸を中心に回転したときのサーフェスの総偏差を測定する。振れには円形振れと総振れの2種類がある。

円形振れ:回転軸に垂直な任意の断面または平面において、回転部品の表面がどれだけ変化するかを測定するもの。

トータル・ランアウト： 回転部品の長手軸方向の表面全体に存在するばらつきを測定すること。真直度やテーパーの不規則性によるものと、円形振れの影響が組み合わされている。

適合公差

フィットは、同じ基本サイズの穴とシャフトの組み合わせの許容範囲の関係です。あるいは、フィットは穴とシャフトのペアリングのクリアランスであるとも言えます。クリアランスはプラスにもマイナスにもなります。クリアランスの大きさによって、対になる2つの部品が互いに独立して移動または回転できるか、あるいは一時的または恒久的に接続されるかが決まります。

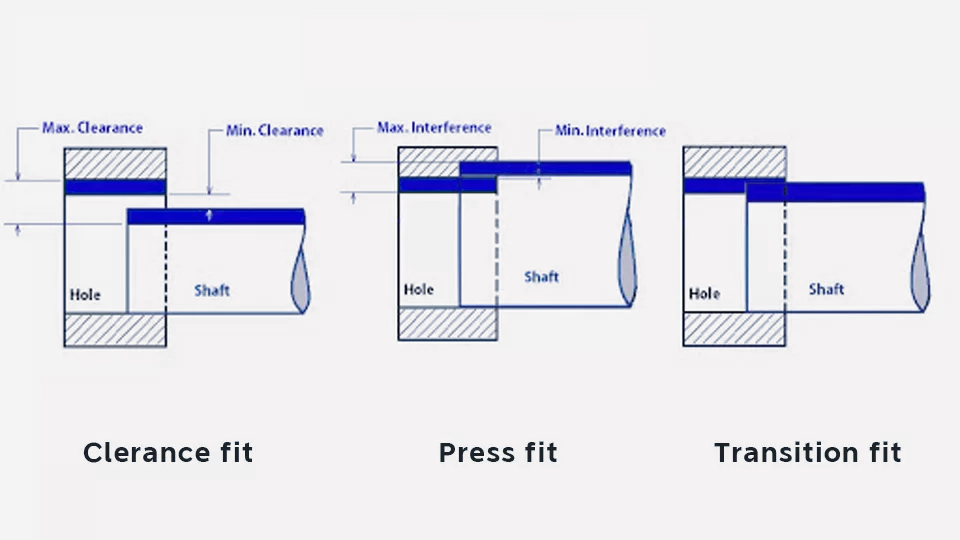
クリアランスフィット、トランジションフィット、トランジションフィットの3種類がある。 プレスフィット(干渉フィット）。

クリアランス・フィット： 穴の許容範囲はシャフトの許容範囲より上であり、言い換えれば、穴はシャフトより大きい。

圧入：つまり、シャフトは穴より大きい。

移行フィット：穴とシャフトの許容範囲が重なること。穴とシャフトのどのペアも、クリアランスまたは圧入を達成することができる。

公差の種類のPDFはこちら、 ダウンロードはこちら

結論

エンジニアリング公差は、設計と製造において基本的な位置を占めている。適切な精度で組み立てられ、どのような製造にもつきものの一定のばらつきがあっても適切に機能する部品が達成されなければなりません。公差は、サイズや形状の許容されるばらつきを定義することで、製品の一貫性と信頼性に貢献します。寸法公差、幾何公差、はめあい公差の異なる種類を理解することは、エンジニアやメーカーにとって、最終製品の機能要件を考慮した上で、さまざまな部品に適切な公差レベルを設定できるようになるために非常に重要です。航空宇宙部品の精度であれ、自動車部品の適合性であれ、公差の適用をマスターすることは、熟練したエンジニアリングと優れた製造の不可欠な部分を形成します。